Phân phối chuẩn là gì? Công thức tính và ứng dụng chi tiết

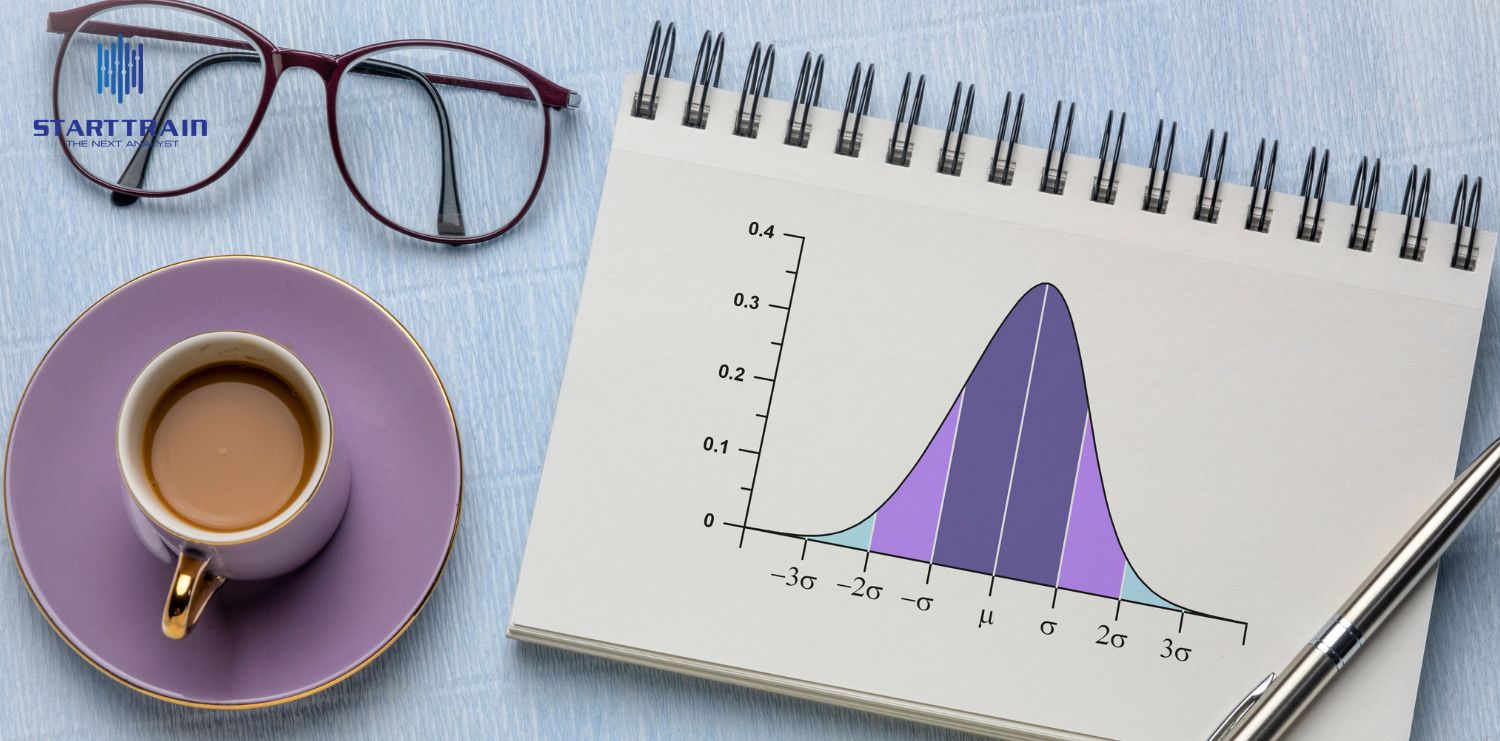
Phân phối chuẩn (hay còn gọi là phân phối Gauss hoặc đường cong hình chuông) là một trong những khái niệm quan trọng và được sử dụng rộng rãi nhất trong xác suất thống kê. Nó mô tả cách mà nhiều hiện tượng tự nhiên, xã hội và kinh tế được phân bổ xung quanh một giá trị trung tâm.

Phân phối chuẩn là gì?

Phân phối chuẩn là một loại phân phối xác suất liên tục cho một biến ngẫu nhiên có biểu đồ tần suất (histogram) hoặc hàm mật độ xác suất (Probability Density Function – PDF) có hình dạng đối xứng hoặc hình chuông (bell-shaped curve).

Ngoài ra, dạng phân phối này còn được biết đến với tên gọi Phân phối Gauss (Gaussian Distribution) trong xác suất thống kê, đặt theo tên nhà toán học Carl Friedrich Gauss.

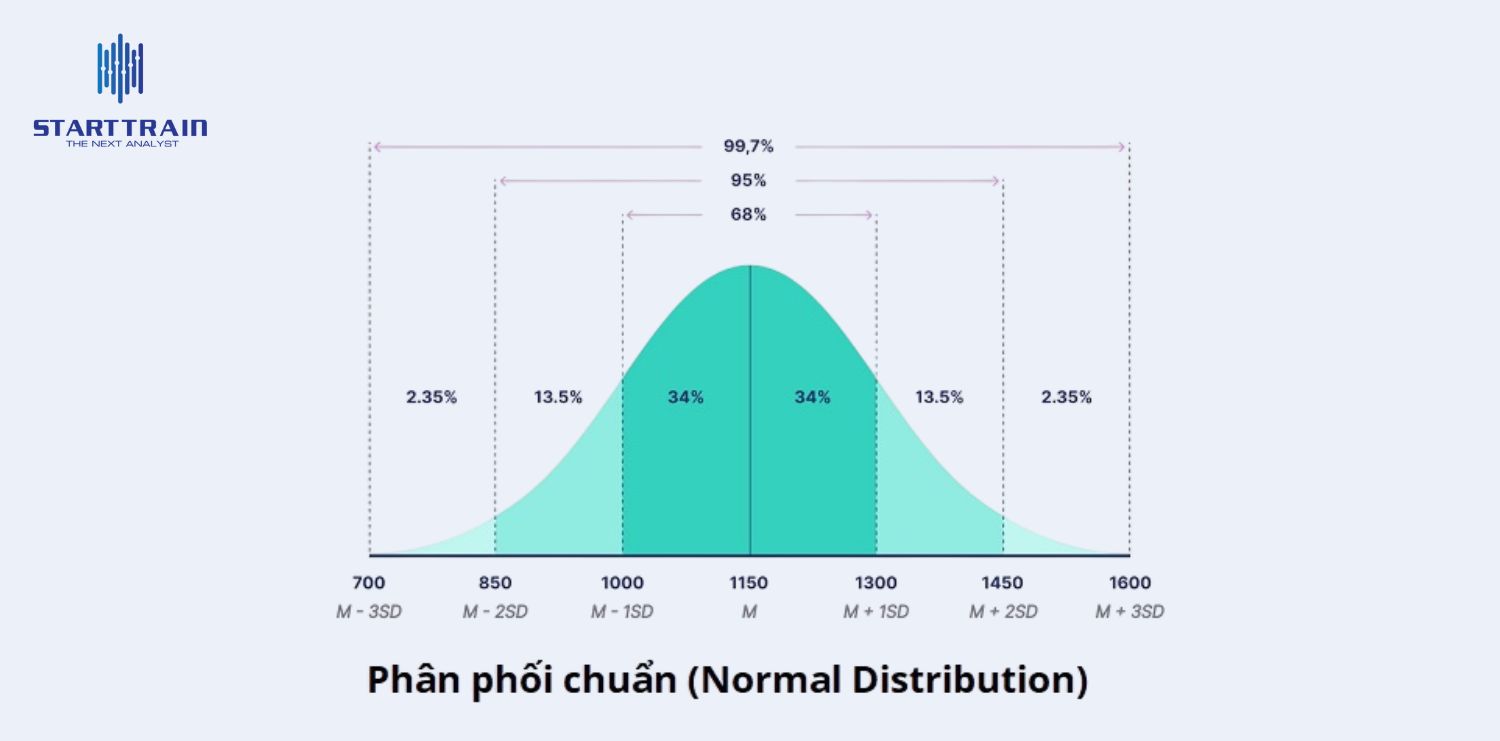
Mô hình phân phối này được đặc trưng hoàn toàn bởi hai tham số:

Kỳ vọng ( μ- Mean): Xác định vị trí trung tâm của đỉnh chuông.
Phương sai (σ² – Variance) hoặc độ lệch chuẩn ( σ – Standard Deviation): Xác định độ rộng (độ trải) của đường cong.

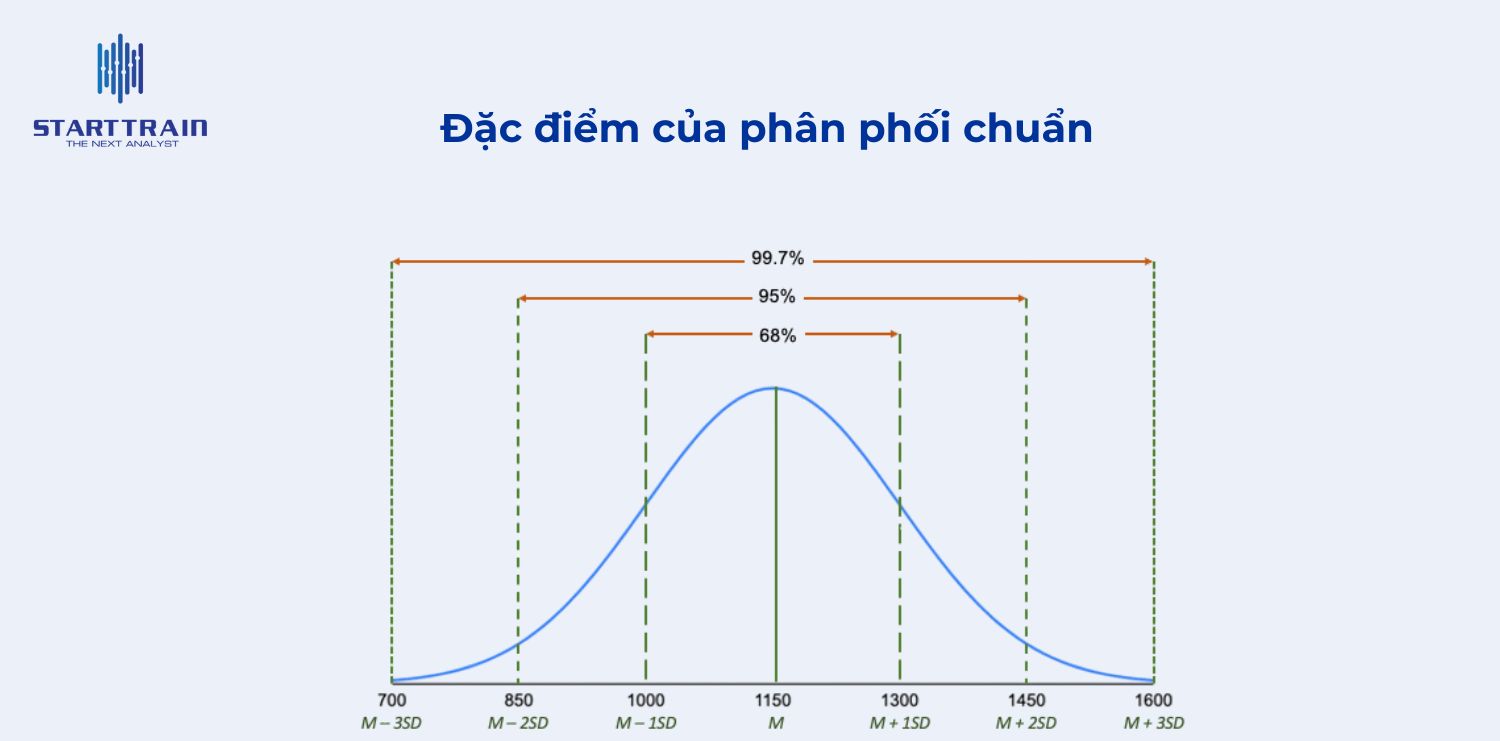
Đặc điểm của phân phối chuẩn

Đối xứng: Đường cong hoàn toàn đối xứng qua giá trị kỳ vọng (). Giá trị trung bình (Mean), trung vị (Median) và tần suất (Mode) đều trùng nhau tại đỉnh của đường cong.
Hình chuông: Đường cong có hình dạng đặc trưng, dốc thoai thoải ở hai bên và đạt đỉnh ở giữa.
Quy tắc 68-95-99.7 (Quy tắc thực nghiệm – empirical rule):
- Khoảng 68.27% dữ liệu nằm trong μ ± 1σ.
- Khoảng 95.45% dữ liệu nằm trong μ ± 2σ.
- Khoảng 99.73% dữ liệu nằm trong μ ± 3σ.
Vô hạn: Đường cong tiệm cận trục hoành khi tiến ra ±∞ nhưng không bao giờ chạm trục hoành.

Công thức tính

Hàm mật độ xác suất

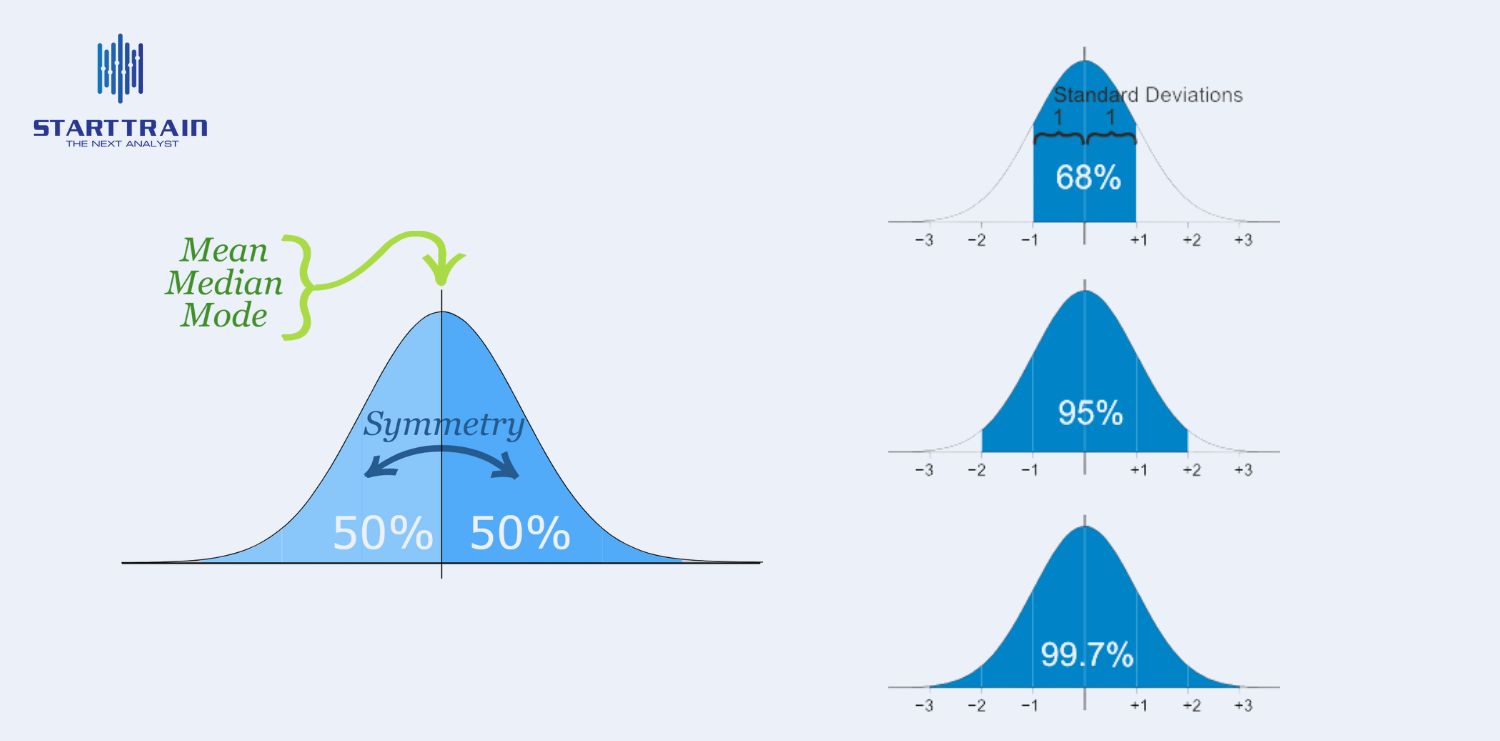
Hàm mật độ xác suất (PDF) của một biến ngẫu nhiên X tuân theo phân phối Gauss với kỳ vọng và phương sai 2 được cho bởi công thức:

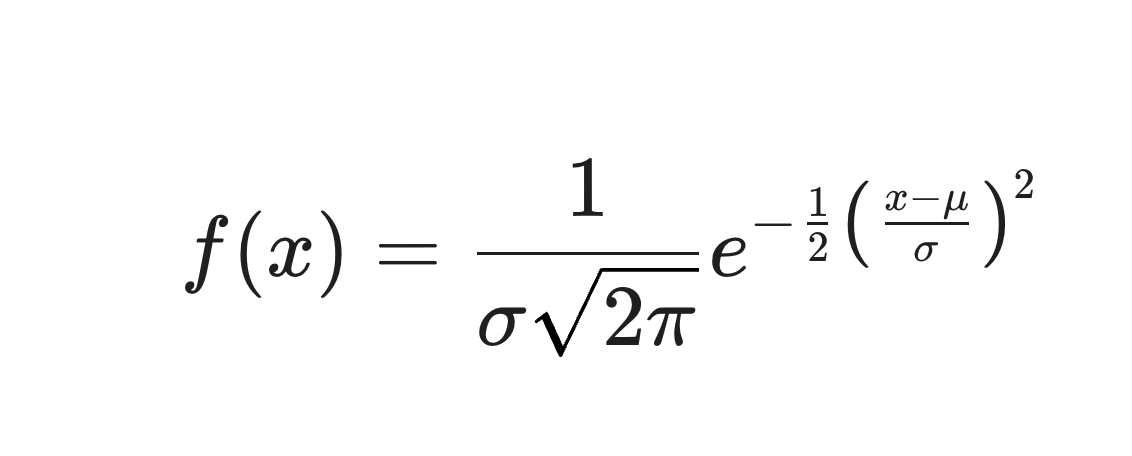
Trong đó:

x: là giá trị của biến ngẫu nhiên.
μ: là kỳ vọng (giá trị trung bình) của phân phối.
σ: là độ lệch chuẩn của phân phối.
π ≈ 3.14159 và e ≈ 2.71828 là các hằng số toán học.

Phân phối chuẩn hóa (Standard Normal Distribution)

Phân phối chuẩn hóa là trường hợp đặc biệt của phân phối chuẩn, ký hiệu ZN(0,1), với:

Kỳ vọng μ = 0
Độ lệch chuẩn σ = 1

Mọi biến ngẫu nhiên X tuân theo phân phối chuẩn đều có thể được chuẩn hóa thành biến Z bằng phép biến đổi Z-score:

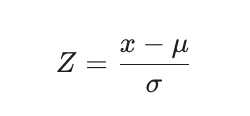
Việc chuẩn hóa này cho phép chúng ta sử dụng bảng Z-score (Standard Normal Table) để tính xác suất cho mọi phân phối chuẩn mà không cần phải tính toán tích phân phức tạp.

Xem thêm: Data Analytics là gì? Có điểm gì khác với Data Analysis

Phân tích độ dốc trong phân phối chuẩn

Độ dốc (Skewness) là một chỉ số đo lường mức độ bất đối xứng của phân phối xác suất của một biến ngẫu nhiên.

Theo định nghĩa, phân phối Gauss là hoàn toàn đối xứng qua giá trị trung bình. Do đó, độ dốc (Skewness) của phân phối chuẩn luôn bằng 0.

Nếu độ dốc > 0 (positive skewness): Phân phối bị kéo dài về bên phải (đuôi dài hơn ở phía dương). Trung vị < Trung bình.
Nếu độ dốc < 0 (negative skewness): Phân phối bị kéo dài về bên trái (đuôi dài hơn ở phía âm). Trung bình < Trung vị.

Việc phân tích độ dốc giúp đánh giá mức độ dữ liệu thực tế gần với giả định phân phối Gauss như thế nào, điều này rất quan trọng trong nhiều kỹ thuật kiểm định giả thuyết thống kê.

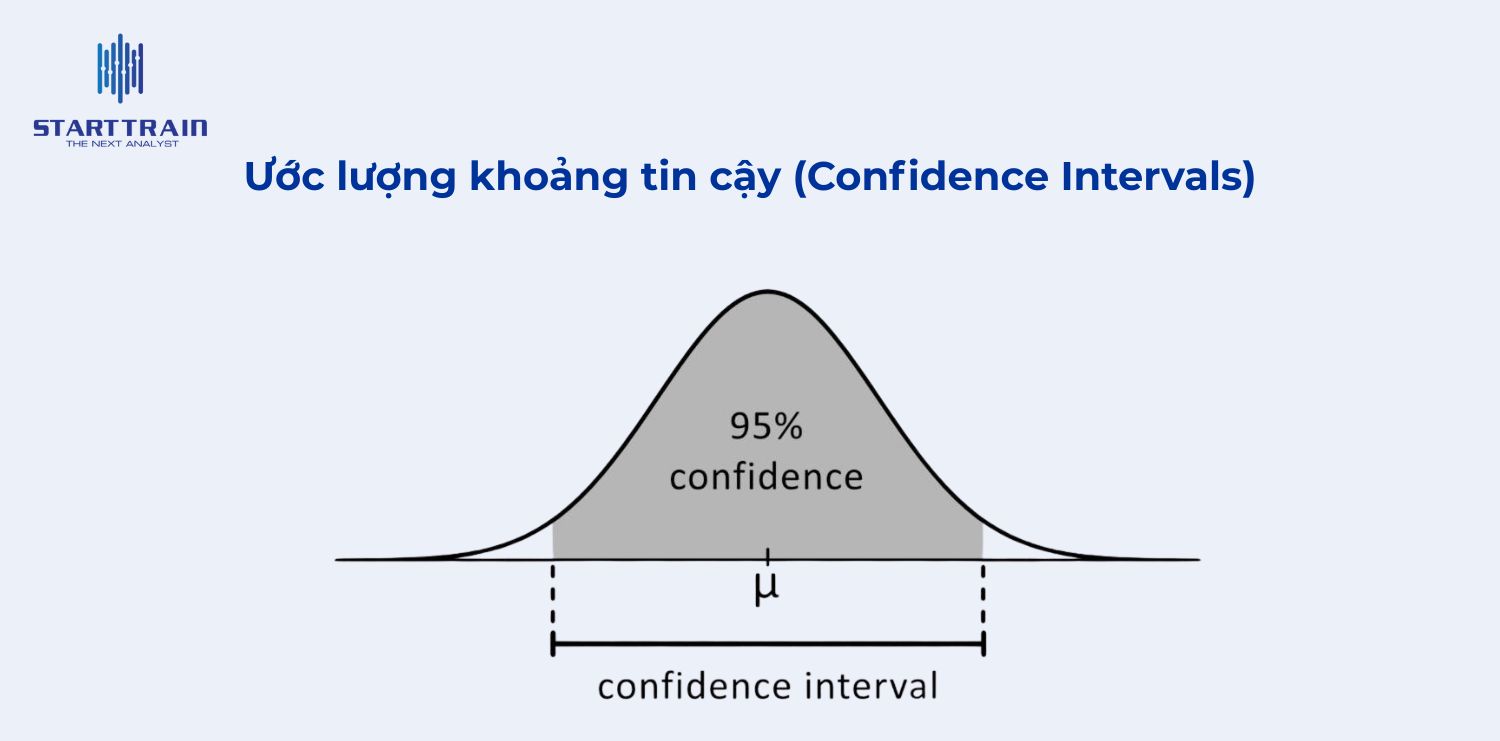
Ứng dụng trong thống kê

Phân phối chuẩn là công cụ không thể thiếu trong thống kê suy luận (Inferential Statistics) giúp chúng ta đưa ra kết luận về một quần thể dựa trên dữ liệu mẫu.

Ước lượng khoảng tin cậy (Confidence Intervals)

Phân phối Gauss được sử dụng để xây dựng khoảng tin cậy cho giá trị trung bình của quần thể. Dựa trên Z-score hoặc T-score (khi n nhỏ), chúng ta có thể xác định một khoảng mà giá trị trung bình thực của quần thể có khả năng nằm trong đó với một mức tin cậy nhất định.

Kiểm định giả thuyết (Hypothesis Testing)

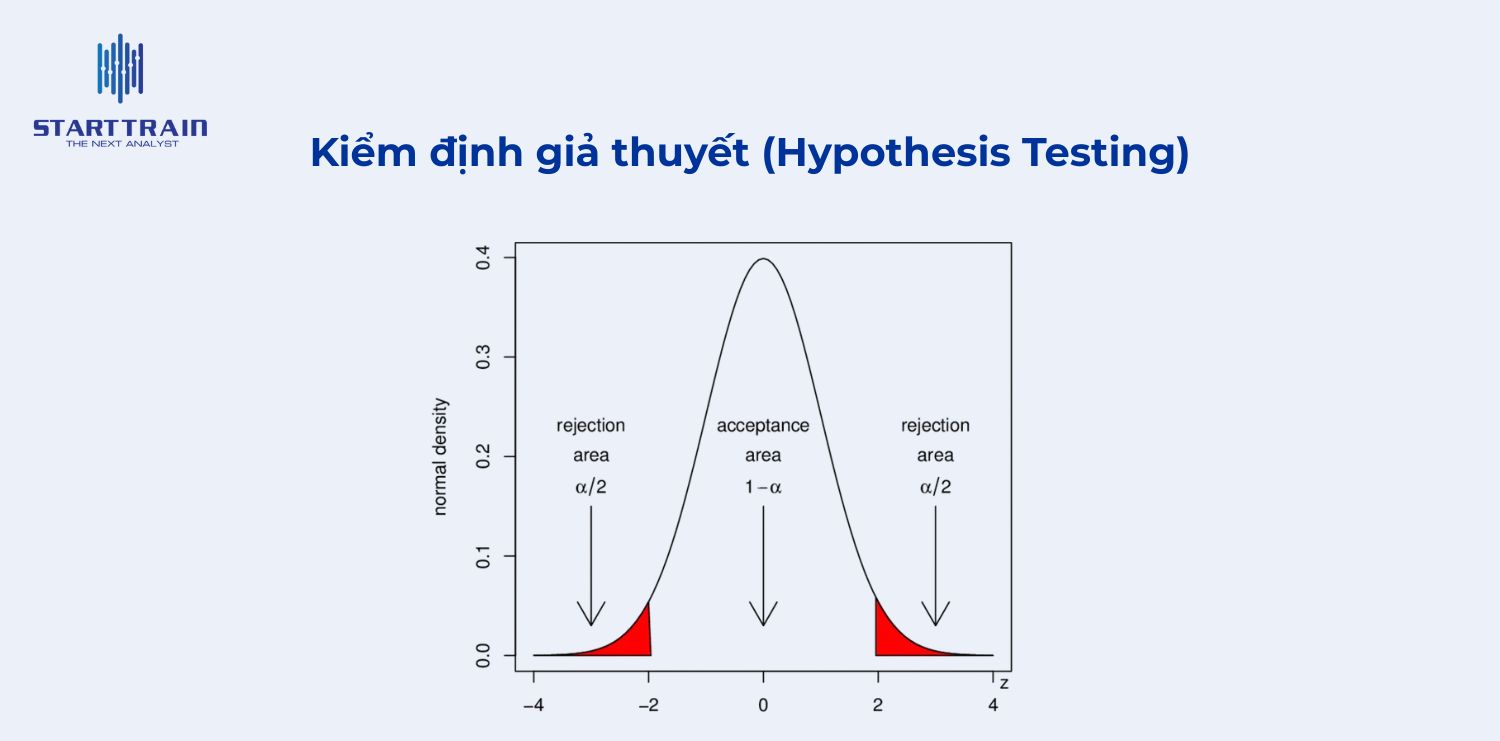
Nhiều kiểm định thống kê phổ biến nhất (như kiểm định Z và kiểm định t) đều dựa trên giả định rằng phân phối của trung bình mẫu là chuẩn (theo CLT). Các kiểm định này giúp xác định liệu sự khác biệt quan sát được giữa các mẫu hoặc giữa mẫu và quần thể có ý nghĩa thống kê hay không.

Ví dụ điển hình về phân phối chuẩn trong thực tế

Phân phối chuẩn là một mô hình thống kê tuyệt vời cho nhiều hiện tượng:

Chiều cao con người: Chiều cao của một nhóm người trưởng thành đồng nhất (cùng giới tính, khu vực) thường tập trung quanh một mức trung bình và phân tán đều về hai phía.
Chỉ số IQ: Chỉ số Thông minh (IQ) được thiết kế để phân phối chuẩn với μ =100 và σ =15.
Sai số đo lường: Sai số ngẫu nhiên trong quá trình đo lường (khoa học, vật lý) thường tuân theo phân phối Gauss.
Kết quả sản xuất: Đường kính, trọng lượng, hay tuổi thọ của sản phẩm được sản xuất hàng loạt thường tập trung quanh giá trị mục tiêu và tuân theo phân phối chuẩn.

Kết luận

Phân phối chuẩn (Normal Distribution) vượt ra ngoài phạm vi của một khái niệm toán học đơn thuần, trở thành một công cụ mô hình hóa mạnh mẽ giúp giải thích sự phân bố của vô số hiện tượng trong thế giới thực.

Tính nền tảng của nó được củng cố nhờ Định lý Giới hạn Trung tâm (CLT). Định lý này khẳng định rằng, phân phối của các giá trị trung bình mẫu sẽ tiến về dạng chuẩn bất kể hình dạng phân phối ban đầu của quần thể. Điều này khiến phân phối chuẩn trở thành mô hình mặc định và là công cụ cơ bản nhất trong thống kê suy luận.

Về mặt ứng dụng, việc hiểu và sử dụng phân phối chuẩn là bước đi quan trọng đầu tiên để chuyển đổi dữ liệu thô thành các quyết định và suy luận có giá trị. Tính ứng dụng của nó bao trùm nhiều lĩnh vực: từ việc xác định chất lượng sản phẩm trong công nghiệp, đánh giá hiệu suất nhân viên, đến phân tích rủi ro tài chính và kiểm định các giả thuyết khoa học.

Cuối cùng, phân phối Gauss tạo ra sự kết nối mạnh mẽ giữa lý thuyết và thực tế. Nhờ khả năng chuẩn hóa dữ liệu (sử dụng Z-score), nó cung cấp một khuôn khổ thống nhất để dễ dàng so sánh các bộ dữ liệu khác nhau, định lượng xác suất và đánh giá độ bất thường của các quan sát. Tóm lại, nắm vững phân phối chuẩn là chìa khóa để mở cánh cửa vào thế giới phân tích và dự đoán bằng thống kê.